a. Định lí thuận
Nếu một đường thẳng cắt hai của một tam giác và song song với cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
(Delta ABC;,,B'C',//BC, Rightarrow frac{{AB'}}{{AB}} = frac{{AC'}}{{AC}}.)
b. Định lí đảo
Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
(Delta ABC;,frac{{AB'}}{{AB}} = frac{{AC'}}{{AC}} Rightarrow B'C'//BC)
Tóm tắt: (Delta ABC;,,B'C'//BC Leftrightarrow frac{{AB'}}{{AB}} = frac{{AC'}}{{AC}}.)
Chú ý: Định lí Talet thuận và đảo đúng với cả ba trường hợp hình vẽ sau:
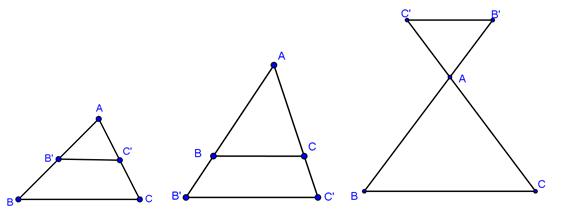
c. Hệ quả
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
(Delta ABC;,,B'C'//BC Rightarrow frac{{AB'}}{{AB}} = frac{{B'C'}}{{BC}} = frac{{C'A}}{{CA}}.)
a. Định lí thuận
Nhiều đường thẳng song song định ra trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
(a//,,b,,//,,c Rightarrow frac{{AB}}{{BC}} = frac{{A'B'}}{{B'C'}})
Chú ý: Ta chứng minh dễ dàng định lí này bằng cách kẻ qua A’ một đường thẳng song song với (Delta ), đường này cắt b, c theo thứ tự tại các điểm B’’ và C’’. Dễ thấy A’B’’ = AB, B’’C’’ = BC. Sau đó, áp dụng định lí Talet trong tam giác vào tam giác A’C’’C’ để có:
(frac{{A'B'}}{{B'C'}} = frac{{A'B''}}{{B''C''}}.)
Từ đây suy ra kết luận.
.png)
b. Định lí đảo
Cho ba đường thẳng a, b, c cắt hai cát tuyến (Delta ,,,Delta ') tại các điểm theo thứ tự A, B, C và A’, B’, C’ thoả mãn đẳng thức tỉ lệ:
(frac{{AB}}{{BC}} = frac{{A'B'}}{{B'C'}})
Và hai trong ba đường thẳng a, b, c là song song với nhau thì đường thẳng còn lại cũng song song với hai đường kia.
(frac{{AB}}{{BC}} = frac{{A'B'}}{{B'C'}}) và (a//b Rightarrow a//b//c)
c. Hệ quả (Các đường thẳng đồng quy cắt hai đường thẳng song song)
- Nhiều đường thẳng đồng quy định ra trên hai đường thẳng song song những đoạn thẳng tương ứng tỉ lệ.
(a//b Rightarrow frac{{AB}}{{A'B'}} = frac{{BC}}{{B'C'}} = frac{{AC}}{{A'C'}}.)
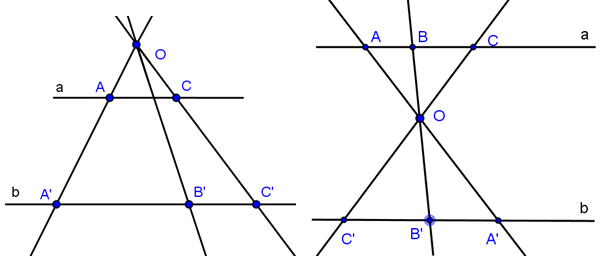
- Ngược lại, nếu nhiều đường thẳng định ra trên hai đường thẳng song song các đoạn thẳng tương ứng tỉ lệ thì chúng đồng quy tại một điểm.
(frac{{AB}}{{A'B'}} = frac{{BC}}{{B'C'}} Rightarrow {rm{AA}}',BB',CC') đồng quy tại O.
Việc chứng minh mệnh đề thuận được dựa trực tiếp vào định lí thuận của định lí Talet
Việc chứng minh mệnh đề đảo thường được nhờ vào phương pháp chứng minh phản chứng.
Chú ý:
1. Người ta thường sử dụng định lí Talet vào việc chứng minh các hệ thức dạng.
(begin{array}{l}frac{a}{b} = frac{c}{d}a.d = b.c{a^2} = b.cend{array})
Nhất là khi trong giả thiết cho ta các đường thẳng song song.
2. Định lí đảo của định lí Talet cho ta một cách chứng minh hai đường thẳng song song.
3. Hệ quả của định lí Talet tổng quá cho ta cách chứng minh các đường thẳng đồng quy.
Ví dụ 1: Cho tam giác ABC. Trên cạnh AC ta lấy hai điểm D, E sao cho AD = DE = EC. Trung tuyến AM cắt BD tại P và trung tuyến CN cắt BE tại Q.
1. Chứng minh điểm Q là trung điểm của trung tuyến CN.
2. Chứng minh PQ // AC.
3. Suy ra (PQ = frac{1}{2}MN) và (PQ = frac{3}{4}DE.)
Giải
.png)
1. Nối AD. Vì N là trung điểm của AB, D là trung điểm của AE nên ND // BE hay QE // ND.
QE // ND mà E là trung điểm của CD nên suy ra Q là trung điểm của CN.
2. Lí luận như trên, ta chứng minh được P là trung điểm của AM.
Gọi G là trọng tâm của tam giác ABC. Như vậy
(AG = frac{2}{3}AM,,,AP = frac{1}{2}AM)
Cho ta (GP = AG - AP = frac{2}{3}AM - frac{1}{2}AM = frac{1}{6}AM)
( Rightarrow frac{{GP}}{{GA}} = frac{1}{6}AM:frac{2}{3}AM = frac{1}{4})
Chứng minh tương tự, ta có:
(frac{{GQ}}{{GC}} = frac{1}{4}) hay (frac{{GP}}{{GA}} = frac{{GQ}}{{GC}} Rightarrow PQ//AC.)
3. PQ // AC mà MN // AC suy ra PQ // MN,
Cho ta (frac{{PQ}}{{MN}} = frac{{GP}}{{GM}} = frac{1}{6}AM:frac{1}{3}AM Rightarrow frac{{PQ}}{{MN}} = frac{1}{2})
( Rightarrow PQ = frac{1}{2}MN)
(PQ = frac{1}{2}MN) mà (MN = frac{1}{2}AC Rightarrow PQ = frac{1}{4}AC)
Vì (PQ = frac{1}{4}AC) và (DE = frac{1}{3}AC Rightarrow frac{{PQ}}{{DE}} = frac{3}{4})
( Rightarrow PQ = frac{3}{4}DE.)
Ví dụ 2: Cho tứ giác lồi ABCD. Đường thẳng qua B và song song với CD cắt AC tại F bà đường thẳng qua C song song với AB cắt BD tại E. Chứng minh EF // AD.
Giải
.png)
Gọi O là giao điểm của hai đường chéo AC và BD
Áp dụng định lí Talet thuận vào tam giác AOB.
(begin{array}{l}EC//AB Rightarrow frac{{OC}}{{OA}} = frac{{OE}}{{OB}} Rightarrow OC.OB = OA.OE,,,,,,,,,,,,,,,,,,(1)end{array})
Áp dụng định lí Talet thuận vào tam giác COD:
(begin{array}{l}FB//DC Rightarrow frac{{OC}}{{{rm{OF}}}} = frac{{OD}}{{OB}} Rightarrow OC.OB = OD.{rm{OF}},,,,,,,,,,,,,,,,,{rm{(2)}}end{array})
Từ (1) và (2) suy ra: (OA.OE = OD.{rm{OF}} Rightarrow frac{{OA}}{{OF}} = frac{{OD}}{{OE}}) (3)
Từ đẳng thức (3) theo định lí Talet đảo, ta có ngay EF // AD.
Ví dụ 3: Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm D, E. Một đường thẳng ({d_1}) qua D cắt cạnh Oy tại điểm F, đường thẳng ({d_2}) đi qua E và song song với ({d_1}), cắt cạnh Oy tại điểm G. Đường thẳng ({d_3})qua G và song song với EF, cắt cạnh Ox tại điểm H. Chứng minh hệ thức: (O{E^2} = OD.OH.)
Giải
.png)
Áp dụng định lí Talet thuận vào tam giác OEG:
(FD,,//,,EG Rightarrow frac{{OD}}{{OE}} = frac{{{rm{OF}}}}{{OG}},,,,(1))
Với tam giác OGH, ta có:
(GH//FE Rightarrow frac{{OF}}{{OG}} = frac{{OE}}{{OH}},,,,(2))
Từ (1) và (2) suy ra: (frac{{OE}}{{OH}} = frac{{OD}}{{OE}} Rightarrow O{E^2} = OD.OH)



